Problemas De Suma De Fracciones Y Ejercicios Resueltos – En este artículo, exploraremos el mundo de la suma de fracciones, brindándote una guía completa con problemas y ejercicios resueltos para que domines este concepto matemático.
Desde la definición de fracciones hasta métodos paso a paso para sumarlas, te guiaremos a través de todo lo que necesitas saber sobre este tema esencial.
Métodos para Sumar Fracciones: Problemas De Suma De Fracciones Y Ejercicios Resueltos

Existen varios métodos para sumar fracciones, cada uno con sus ventajas y desventajas. Los métodos más comunes incluyen:
Método del mínimo común múltiplo (MCM)
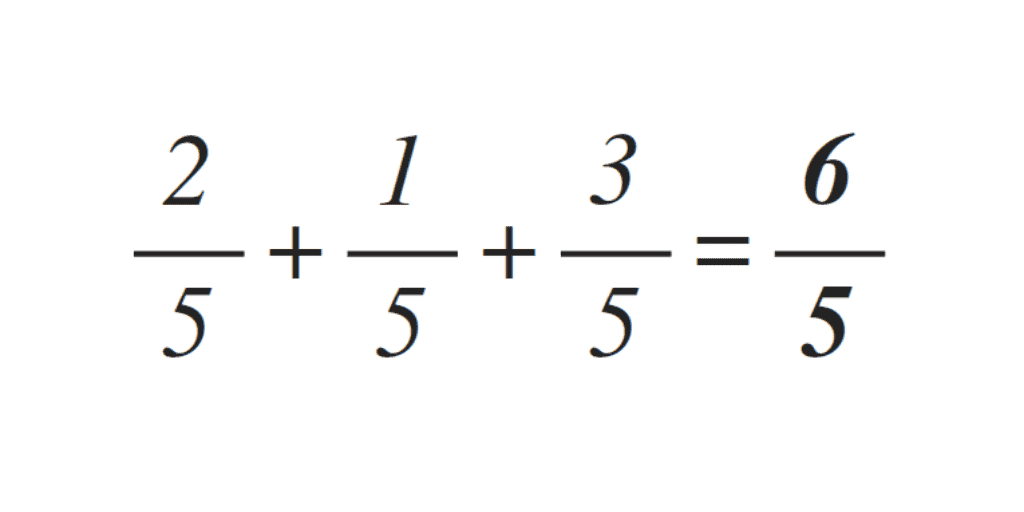
El método del MCM implica encontrar el mínimo común múltiplo de los denominadores de las fracciones y luego convertir cada fracción a una fracción equivalente con el MCM como denominador. Una vez que todas las fracciones tienen el mismo denominador, se pueden sumar los numeradores y el denominador común se mantiene.
Por ejemplo, para sumar las fracciones 1/2 y 1/3, primero encontramos el MCM de 2 y 3, que es
6. Luego, convertimos 1/2 a 3/6 y 1/3 a 2/
6. Finalmente, sumamos las fracciones: 3/6 + 2/6 = 5/6.
Método de las fracciones equivalentes, Problemas De Suma De Fracciones Y Ejercicios Resueltos

El método de las fracciones equivalentes implica encontrar una fracción equivalente para una o ambas fracciones que tengan el mismo denominador. Una vez que las fracciones tienen el mismo denominador, se pueden sumar los numeradores y el denominador común se mantiene.
Por ejemplo, para sumar las fracciones 1/2 y 1/4, podemos encontrar una fracción equivalente para 1/2 que tenga un denominador de 4, como 2/
4. Luego, podemos sumar las fracciones: 2/4 + 1/4 = 3/4.
Método de la multiplicación cruzada
El método de la multiplicación cruzada implica multiplicar el numerador de cada fracción por el denominador de la otra fracción. Los productos se suman y el resultado se convierte en el numerador de la fracción resultante. El denominador de la fracción resultante es el producto de los dos denominadores originales.
Por ejemplo, para sumar las fracciones 1/2 y 1/3, multiplicamos 1 por 3 y 2 por 1. Los productos son 3 y 2, que se suman a 5. El denominador de la fracción resultante es el producto de 2 y 3, que es 6. Por lo tanto, la suma de las fracciones es 5/6.
Esperamos que esta guía te haya proporcionado una comprensión clara de la suma de fracciones. Recuerda practicar regularmente para mejorar tus habilidades y aplicar estos conocimientos en situaciones prácticas.
